Defining “complicated” state-space models¶
Some users reported difficulties with defining “complicated” state-space models, that is models where the variables \(X_t\) and \(Y_t\) may:
be multivariate;
have non-standard distributions;
have “named” components (such as “S” /”I” / “R” for the number of susceptible / infected / recovered cased in a SIR model), and the user would like the specify the model accordingly.
be missing at certain times.
This tutorial explains how to deal with such issues.
Before we start¶
Note that if you are only interested in implementing the bootstrap filter associated to your model, and if the following tasks are easy to implement:
writing a simulator that samples (\(N\) times) from the distribution of \(X_t\) given \(X_{t-1}\);
writing a function that computes the log of density \(f(y_t|x_t)\) of data-point \(y_t\) given \(X_t=x_t\), for an array of \(N\) particles \(X_t^n\);
then one option is to implement manually the corresponding Feynman-Kac object that describes that bootstrap filter. See the previous tutorial.
Multivariate state-space models (with conditional independent distributions)¶
The bearings-only model is a famous (toy) tracking model. The tracked object (e.g. a ship) moves according to a 2D motion model, where the speed evolves according to a random walk. State \((X_t)\) is 4-dimensional, the first two components give the position, the next two give the velocity, and one has:
Note in particular that the first two components (the position in Cartesian coordinates) are deterministic functions of \(X_{t-1}\).
Furthermore, ones observes some radar measurement, that gives the direction (angle) of that object, up to some noise:
Here how you may define such a model; pay particular attention to method PX.
[8]:
from matplotlib import pyplot as plt
import particles
from particles import distributions as dists
from particles import state_space_models as ssms
class BearingsOnly(ssms.StateSpaceModel):
""" Bearings-only tracking SSM.
"""
default_params = {'sigmaX': 2.e-4,
'sigmaY': 1e-3,
'x0': np.array([3e-3, -3e-3, 1., 1.])
}
def PX0(self):
return dists.IndepProd(dists.Dirac(loc=self.x0[0]),
dists.Dirac(loc=self.x0[1]),
dists.Normal(loc=self.x0[2], scale=self.sigmaX),
dists.Normal(loc=self.x0[3], scale=self.sigmaX),
)
def PX(self, t, xp):
return dists.IndepProd(dists.Dirac(loc=xp[:, 0] + xp[:, 2]),
dists.Dirac(loc=xp[:, 1] + xp[:, 3]),
dists.Normal(loc=xp[:, 2], scale=self.sigmaX),
dists.Normal(loc=xp[:, 3], scale=self.sigmaX),
)
def PY(self, t, xp, x):
angle = np.arctan(x[:, 0] / x[:, 1])
angle[x[:, 1] < 0.] += np.pi
return dists.Normal(loc=angle, scale=self.sigmaY)
bear = BearingsOnly(sigmaX=0.5)
x, y = bear.simulate(30)
xarr = np.array(x).squeeze()
plt.plot(xarr[:, 0], xarr[:, 1])
[8]:
[<matplotlib.lines.Line2D at 0x7f63da280880>]
The following points are noteworthy:
Since the components of \(X_t\) are independent (conditional on \(X_{t-1}\)) we specify the distribution of \(X_t\) as a product of independent distributions, through
dists.IndepProd. This particular object takes as input an arbitrary number (2 or more) of univariate distributions, and combines then to define a joint distribution.Since the state-space is \(\mathbb{R}^4\), the particles will be stored in a numpy array of shape (N, 4): e.g. first component will be in
x[:, 0]. (Recall that python uses zero-based indexing.)The probability distributions implemented in
particles“operate on arrays”: whenever a parameter of that distribution varies across particles, one should specify that parameter as an array. For instance, when we want to specify that \(X_t[3] | X_{t-1} \sim N(X_{t-1}[3],\sigma_X^2)\) we must define a Gaussian distribution, where the mean (parameterloc) is set toxp[:, 2], the array that contains the \(N\) possible values of component \(X_{t-1}[3]\).
Non-independent joint distribution, named components¶
Of course, the big limitation of dists.IndepProd is that it does not let you specify joint distributions where components are not independent. For this, you may use “structured distributions” (dists.StructDist). A nice extra is that it makes it possible to name components.
Structured distributions were designed initially to specify prior distributions for parameters, but nothing prevents you from using them in the definition of a state-space model. Recall that structured distributions are intimately linked to structured arrays; e.g. when you simulate from a structured distribution, you get a structured array with the same keys. Have a quick look here if you are not familiar already with structured arrays and structured distributions.
Here is a silly example: Suppose that you have a state-space model where \(X_t=(A_t, B_t)\), and \begin{align*} A_t & \sim N(A_{t-1}, 1) \\ B_t & = B_{t-1} + A_t \end{align*}
In words, \(B_t\) is the cumulative sum of process \(A_t\). We may specify a state-space model with such a process as follows:
[2]:
def abdist(xp): # xp means X_{t-1}
d = {'a': dists.Normal(loc=xp['a']),
'b': dists.Cond(lambda x: dists.Dirac(xp['b'] + x['a']))}
return dists.StructDist(d)
class SillyModel(ssms.StateSpaceModel):
def PX0(self):
return abdist({'a': 0., 'b': 0.})
def PX(self, t, xp):
return abdist(xp)
def PY(self, t, xp, x):
return dists.Normal(loc=x['a'], scale=0.3) # whatever
silly = SillyModel()
x, y = silly.simulate(30)
plt.style.use('ggplot')
plt.plot([xt['a'] for xt in x], label=r'$a_t$')
plt.plot([xt['b'] for xt in x], label=r'$b_t$')
plt.legend()
[2]:
<matplotlib.legend.Legend at 0x7f63da991b20>
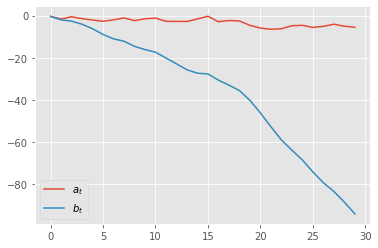
Let’s unpack things:
dists.StructDisttakes as input a dict-like object; keys are the names of the components, and values are their distributions.Component
'a'has a certain distribution (here, a Gaussian centred on \(A_{t-1}\)).Component
'b'is assigned a conditional distribution: thedists.Condobject takes as input a function, which for a given inputx, returns the conditional distribution for that value ofx. Note the role playedx: it is a structured array such thatx[f]returns \(N\) value for any componentf(here'a') whose distribution has already been defined.More generally, you may implement any kind of chain rule decomposition with
StructDist; e.g; you could introduce a componentcwhose distribution would depend onaandb, and so on. One important point: these components should defined in order; i.e. if the distribution of'c'depends on'a'and'b', then'a'and'b'must be defined previously.Technical point: since Python 3.6, dictionaries preserve order (they remember you defined them with keys ordered in a certain way). If you use an older version of Python, you might need to use ordered dictionary, as explained in the documentation of
StructDist.
Arbitrary distributions¶
With dists.IndepProd and dists.StrucDist you can create many complicated multivariate distributions out of simple univariate distributions. Many standard univariate distributions are defined in module distributions. Note you can also define many more by using transformations, e.g:
[3]:
# law of Y=log(X), X~Gamma(2, 2)
dist_log_gam = dists.LogD(dists.Gamma(a=2., b=2.))
x = dist_log_gam.rvs(size=1000)
plt.hist(x, 40);
Finally, it is always possible to create your own (univariate or multivariate) probability distributions, by sub-classing the base class ProbDist; see the documentation of the module for more information.
Missing data¶
We are going to consider two slightly different scenarios for missing data.
Missing at fixed times¶
Suppose we know in advance that the observation \(Y_t\) will be missing at certain times \(t\); e.g. every Sunday for daily data. In that case, we may use the dists.FlatNormal distribution as follows.
[4]:
class ToyModelWithMissingData(ssms.StateSpaceModel):
default_params = {'sigmaX': 1., 'sigmaY': 0.2}
def PX0(self):
return dists.Normal(scale=self.sigmaX)
def PX(self, t, xp):
return dists.Normal(loc=xp, scale=self.sigmaX)
def PY(self, t, xp, x):
if t % 7 == 0: # Sunday
return dists.FlatNormal(loc=x)
else: # Other days
return dists.Normal(loc=x, scale=self.sigmaY)
dists.FlatNormal behaves like a Normal distribution with infinite variance: its log-density is flat (=zero). The model above is simply going to ignore the value of data[t] for any \(t\) that is a multiple of seven.
Missing at random times¶
In case you don’t want to specify in advance at which times the data may be missing, you may use instead dists.MixMissing. This distribution represents a mixture distribution, where:
with probability
pmiss, the outcome is ‘missing’ (represented by valueNaN).with probability `1. - pmiss`, the outcome follows a certain base distribution.
[5]:
class ToyModelWithMissingDataRandomTimes(ssms.StateSpaceModel):
default_params = {'sigmaX': 1., 'sigmaY': 0.2}
def PX0(self):
return dists.Normal(scale=self.sigmaX)
def PX(self, t, xp):
return dists.Normal(loc=xp, scale=self.sigmaX)
def PY(self, t, xp, x):
return dists.MixMissing(pmiss=0.20,
base_dist=dists.Normal(loc=x, scale=self.sigmaY))
Now, if you simulate from this model, you get a Nan with probability 20% at any given time step.
[9]:
toymod = ToyModelWithMissingDataRandomTimes()
x, y = toymod.simulate(10)
print(np.array(y))
[[ 1.15719099]
[ 1.12199113]
[ 2.47971689]
[ 2.74431727]
[ 0.84142741]
[ 1.10468696]
[ nan]
[-0.70324617]
[ nan]
[ 0.19505344]]
Then, when a particle filter is run, each Nan in the data is treated as a missing observation, and is treated as such.
[11]:
fk = ssms.Bootstrap(ssm=toymod, data=y)
alg = particles.SMC(fk=fk, N=100, verbose=True)
alg.run()
t=0: resample:False, ESS (end of iter)=13.63
t=1: resample:True, ESS (end of iter)=26.37
t=2: resample:True, ESS (end of iter)=14.31
t=3: resample:True, ESS (end of iter)=19.71
t=4: resample:True, ESS (end of iter)=5.47
t=5: resample:True, ESS (end of iter)=22.68
t=6: resample:True, ESS (end of iter)=100.00
t=7: resample:False, ESS (end of iter)=8.63
t=8: resample:True, ESS (end of iter)=100.00
t=9: resample:False, ESS (end of iter)=21.27
Note in particular how the ESS stays equals to 100 (the maximum value, since \(N=100\)) at times where a Nan was observed.
Technical point: the normalising constant estimate takes into account the probability that you have a missing value; e.g. if your data consist of 10 Nans, the estimate equals \(p^{10}\), where \(p\) is the missing probability.
Multivariate observations with missing data¶
The examples above assume that the observations \(Y_t\) are univariate, but you can combine FlatNormal or MixMissing with dists.IndepProd to specify a model where components of \(Y_t\) may be missing. For instance:
[16]:
class MultivariateModelWithMissingData(ssms.StateSpaceModel):
def PX0(self):
return dists.IndepProd(dists.Normal(),
dists.Normal())
def PX(self, t, xp):
return dists.IndepProd(dists.Normal(loc=xp[:, 0]),
dists.Normal(loc=xp[:, 1]))
def PY(self, t, xp, x):
return dists.IndepProd(dists.Normal(loc=x[:, 0]),
dists.MixMissing(pmiss=0.20,
base_dist=dists.Normal(loc=x[:,0])))
In this model, only the second component of \(Y_t\) may be missing, with probability \(20\%\):
[27]:
ssm = MultivariateModelWithMissingData()
x, y = ssm.simulate(10)
print(np.squeeze(y))
[[-1.65844712 nan]
[-0.47070688 -1.0353565 ]
[ 1.99688692 1.46915379]
[-0.54656891 0.68420457]
[ 1.06249224 1.62856419]
[ 0.93699561 -1.67133867]
[-1.21527128 -0.65343266]
[-4.56505231 -3.10377106]
[-6.88535672 nan]
[-7.42773445 -5.51978829]]
Questions?¶
This tutorial was written to answer some recurring questions from users; if you feel you are still unable to implement your model, feel free to get in touch with the author of the package.